数组中常见的算法

数组元素的赋值（杨辉三角、会行数等）

求数值型数组中元素的最大值、最小值、平均数、总和等

package com.eachwang.java;

public class Test01 {
	public static void main(String[] args) {
		// 创建数组
		int[] arr = new int[6];

		// 生成数据
		for (int i = 0; i < arr.length; i++) {
			arr[i] = (int) (Math.random() * 89 + 10);
		}

		// 遍历数据
		for (int i = 0; i < arr.length; i++) {
			System.out.print(arr[i] + "\t");
		}
		System.out.println();

		// 最大值
		int maxNumber = arr[0];
		for (int i = 1; i < arr.length; i++) {
			maxNumber = (maxNumber > arr[i]) ? maxNumber : arr[i];
		}
		System.out.println("最大值：" + maxNumber);

		// 最小值
		int minNumber = arr[0];
		for (int i = 1; i < arr.length; i++) {
			minNumber = (minNumber < arr[i]) ? minNumber : arr[i];
		}
		System.out.println("最小值：" + minNumber);

		// 总和
		int sum = 0;
		for (int i = 0; i < arr.length; i++) {
			sum += arr[i];
		}
		System.out.println("总和：" + sum);

		// 平均数
		int avg = sum / arr.length;
		System.out.println("平均值：" + avg);
	}
}

数组的赋值、翻转、查找（线性查找、二分法查找法）

赋值

1. 声明两个int类型一维数组arr1和arr2
2. 给arr1赋值数据{1,3,5,7,9,11,13} 
3. 将arr1 赋值 arr2
4. 将arr2中所有的偶数下标中的数据改成下标 
5. 遍历arr1

public class Test02 {
	public static void main(String[] args) {
		// 声明两个int类型一维数组。arr1和arr2，
		int[] arr1, arr2;
		// 给arr1赋值数据{1,3,5,7,9,11,13}
		arr1 = new int[] { 1, 3, 5, 7, 9, 11, 13 };
		for (int i = 0; i < arr1.length; i++) {
			System.out.print(arr1[i] + "\t");
		}
		System.out.println();

		// 将arr1 赋值 arr2
		arr2 = arr1;
		// 将arr2中所有的偶数下标中的数据改成下标
		for (int i = 0; i < arr2.length; i += 2) {
			arr2[i] = i;
		}

		// 遍历arr1
		for (int i = 0; i < arr1.length; i++) {
			System.out.print(arr1[i] + "\t");
		}
	}
}

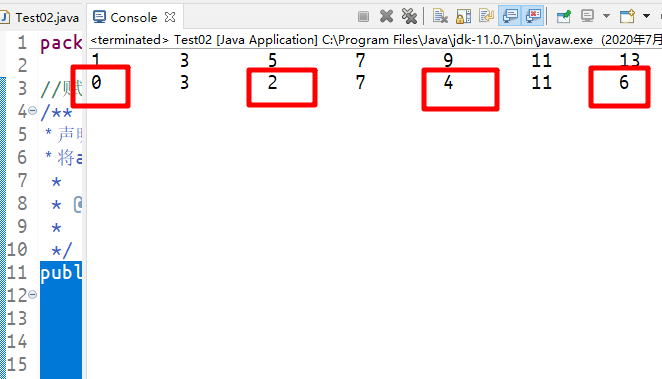
通过结果，我们发现给arr2中修改的数据，arr1中全部修改了。原因就是arr2=arr1，只是将内存地址值赋值过去，他们两个指向的是同一块内存空间

正确的赋值：

		arr2 = new int[arr1.length];
		for (int i = 0; i < arr1.length; i++) {
			arr2[i] = arr1[i];
		}

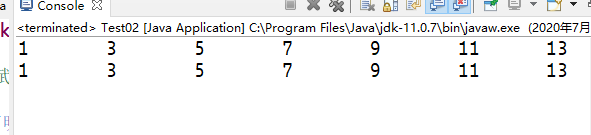
这样，修改了arr2的值后，arr1的值没有变化。

翻转

public class Test03 {
	public static void main(String[] args) {
		int[] arr1 = new int[] { 1, 3, 5, 7, 9, 11, 13 };
		// 翻转
		for (int i = 0; i < arr1.length / 2; i++) {
			int temp = arr1[i];
			arr1[i] = arr1[arr1.length - 1 - i];
			arr1[arr1.length - 1 - i] = temp;
		}

		// 遍历
		for (int i = 0; i < arr1.length; i++) {
			System.out.println(arr1[i]);
		}
	}
}

查找（线性查找、二分法查找法）

####　线性查找

二分法查找法

数组元素的排序算法